ANÁLISIS DE LAS CURVAS DE INFILTRACIÓN PARA DETERMINAR CAUDALES MÁXIMOS EN ZONAS DE ESCASA INFORMACIÓN ANTE EVENTOS EXTREMOS

ANALYSIS OF INFILTRATION CURVES TO DETERMINE MAXIMUM FLOWS IN SCARCE ZONES INFORMATION ABOUT EXTREME EVENTS

Guillermo Gustavo Arriola Carrasco¹

Luis Mariano Villegas Granados²

Gioconda del Socorro Sotomayor Nunura³

Fecha de recepción: 10 junio 2020

Fecha de aceptación: 10 julio 2020

Resumen

La presente investigación tiene como fin la determinación de los caudales máximosen las zonasalejadas de una cuenca donde no se cuenta con información pluviométrica ni hidrométricaempleando el análisis de las curvas de infiltración considerando como primer dato de entrada el método del número de curva. La metodología que se empleó consideró todos los valores de infiltración obtenidos en ciertas partes de la cuenca a partir del muestreo de campo de los diversos tipos de suelos y de los pocos registros históricos de las estaciones pluviométricas llamadas así como subcuencas para el análisis hidrológico y luego se aplicó el procesamiento de imágenes con la ayuda del programa NewLoc Clim v. 1.10 cuyos resultados nos permitieron identificar todos los lugares vulnerables ante fuertes crecidas.

Palabras claves: Escorrentía, caudal máximo, número de curva, infiltración.

Abstract

The purpose of this research is to determine the maximum flow rates in the remote areas of a basin where there is no rainfall or hydrometric information using the analysis of infiltration curves, considering the curve number method as the first input. The methodology that was used considered all the infiltration values ​​obtained in certain parts of the basin from the field sampling of the different types of soils and from the few historical records of the so-called pluviometric stations as well as sub-basins for the hydrological analysis and then Image processing was applied with the help of the New Loc Clim v. 1.10 program whose results allowed us to identify all the vulnerable places in the face of strong floods.

Key Words: Runoff, maximum flow, curve number, infiltration.

1. Introducción

En la actualidad la gran variabilidad de climas que muestra el territorio mundial presenta una infinidad de peligros cuyos impactos económicos son difíciles de superar al corto plazo. En dicha contrastación se pueden deducir que las áreas de mayor impacto ante estos cambios son los países más vulnerables como por ejemplo los de Sudamérica. El Perú no es ajeno a esta realidad pues el problema es latente en todas las regiones y esto es debido a la aleatoriedad de los componentes hidrológico, hidráulico, geológico y geotécnico de las cuencas hidrográficas sobretodo en el norte peruano cuyos cambios se dan principalmente en los meses de verano.

Según los antecedentes de estudio de caudales máximos de las cuencas de la región Lambayequese debe requerir que los estudios contemplenevaluaciones integrales de los recursos hídricos con un mayor énfasis en los ensayos de campo y validación de resultados propios de cada zona de estudio.

_________________________________

¹ Ingeniero Civil, Escuela de Ingeniería Civil, Facultad de Ingeniería, Arquitectura y Urbanismo, Universidad Señor de Sipán, Pimentel - Chiclayo, Perú, garriola@crece.uss.edu.pe. https://orcid.org/0000-0002-2861-1415

² Magíster en Gestión Pública, Escuela de Ingeniería Civil, Facultad de Ingeniería, Arquitectura y Urbanismo, Universidad Señor de Sipán, Pimentel - Chiclayo, Perú, vgranadoslm@crece.uss.edu.pe. https://orcid.org/0000-0001-5401-2566

³Doctora en Ciencias de la Educación, Facultad de Ingeniería, Arquitectura y Urbanismo, Universidad Señor de Sipán, Pimentel - Chiclayo, Perú, giocondasn@crece.uss.edu.pe. https://orcid.org/0000-0001-6082-0893

El objeto de estudio que se planteó es la cuenca hidrográfica del río Chancay desdesus nacientes en el distrito de Chugur en las inmediaciones del río Tacamache a casi 4000 m.s.n.m. hasta las inmediaciones de la bocatoma Racarrumi a 280 m.s.n.m., debido a que es el único lugar de la cuenca con que cuenta con mediciones de caudales desde el año de 1965 hasta la actualidad. Una vez analizados los caudales máximos para la cuenca en mención se aplicó el método del Número de curva, pues el método incluye parámetros importantes que muy poco son empleados en estudios hidrológicos, además el análisis implicó el uso de HecHms y el New Loc Clim para finalmente comparar dichos resultados con los probables eventos extremos.

Los objetivos que se platearon para el buen desarrollo de la investigación versaron en analizar las curvas de infiltración en las zonas de escasa información ante un eventual Fenómeno El Niño considerado como un probable evento extremo y luego los objetivos específicos, comenzando con la recolección, selección y tratamiento de la información disponible y de las características propias de la cuenca, también se realizó el procesamiento estadístico de los caudales y precipitacionespara determinar la mejor bondad de ajusteteórico y gráfico incluyendo los valores respectivos del número de curva considerando además las curvas de infiltración de los muestreos con datos de campoy finalmenteel nivel de aproximación que brinda los softwares por medio del modelo hidrológico de la cuenca denominado precipitación - escorrentía, lo cual permitirá diseñar las diversas estructuras hidráulicas en las zonas de escasa información.

2.Materiales y Métodos

Se empleó la metodología inductiva y deductiva, es decir partiendo de lo general a lo particular, que implicó actividades de campo con las respectivas mediciones y de trabajos de gabinete empleando los programas como el HecHms v3.5, AutoCAD 2014, NewLoc Clim v.1.10. A partir de dicho análisis la hipótesis que se planteó fue empleando las curvas de infiltración se podrán determinar adecuadamente los caudales máximos para la Cuenca del río Chancay en zonas con escasa información considerando diferentes períodos de ocurrencia y de retorno. Para el análisis estadístico se necesitó las precipitaciones ycaudalesde las estaciones pluviométricas e hidrométricas de la cuenca del río Chancay y en el caso de las estaciones (subcuencas) que no tienen información se ha utilizado las curvas de infiltración para determinar la capacidad de suelo de producir escorrentía superficial y subterránea, de acuerdo a ello se determinó las zonas de mayor potencial en producir un caudal máximo sobre todo en zonas donde no se dispone de información.

Conocido el comportamiento del régimen hidrológico de la cuenca, se procedió con el desarrollo de la propuesta de investigación empleando las curvas de infiltración, para ello se realizaron ensayos de campo para medir la infiltración, principal parámetro para estimar la condición hidrológica de los suelos según la clasificación A, B, C y D, tal como se muestra en la figura1.

Los métodos que permitieron determinar las curvas de infiltración son el de Kostiakov, Horton y de Green – Ampt. El procedimiento de campo consistió en saturar una porción de suelo limitado por dos anillos concéntricos denominados “Anillos de Munz” que permitieron medir la variación del nivel del agua en el cilindro interior y por último se graficaron los resultados, se obtuvieron las ecuaciones y factores de mejor ajuste

3. Resultados

Los resultados permitieron determinarlos caudales máximos en las zonas donde no se dispone de información hidrométrica ni pluviométrica,sin embargo,se ha contrastado con los datos de las estaciones disponibles para un mejor análisis de los resultados. La clasificación del suelo permitió a través del programa NewLoc Clim v.1.10 (Local climate estimator – FAO 2006), obtener las características de uso, grupo hidrológico, condición de humedad antecedente y demás parámetros necesarios para luego ingresarlos al programa HecHms.

Tabla 1

Resumen de las precipitaciones máximas de las estaciones pluviométricas del área de influencia de la cuenca del río Chancay obtenidos del análisis de extremos.

Fuente: Elaboración propia.

La tabla 1 muestra los resultados de las precipitaciones máximas ajustadas a las distribucionesteóricas Gumbel Tipo I y Logaritmo Pearson Tipo III para los diferentes períodos de retorno con respecto a cada registro histórico de las estaciones Lambayeque, Ferreñafe, Chiclayo, Pucalá, Tinajones, Reque y Pimentel pertenecientes a la cuenca del río Chancay.

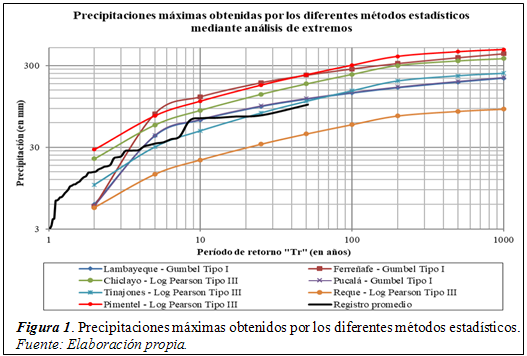
La figura 1 indica que los resultados de las precipitaciones máximas ajustadas a las distribuciones teóricas Gumbel Tipo I y Logaritmo Pearson Tipo III para los diferentes períodos de retorno con respecto a cada registro histórico promedio de las estaciones Lambayeque, Ferreñafe, Chiclayo, Pucalá, Tinajones, Reque y Pimenteltienden a tener valores extremos debido al aumento del período de retorno. Esto se debe a que en algunos años de los registros históricos se presentaron valores atípicossobre todo en los eventos de máximas lluvias. Además, se observó que la estación Reque es la única que presenta valores extremos menores respecto al registro promedio de todas las estaciones consideradas en la presente investigación.

Tabla 2

Resumen de los caudales máximos de la estación hidrométrica Racarrumi del área de influencia de la cuenca del río Chancay obtenidos del análisis de extremos.

Fuente: Elaboración propia.

La tabla 2muestra los resultados de los caudales máximos ajustados a las distribuciones teóricas Nash, Lebediev, Logaritmo Pearson Tipo III y Gumbel Tipo I, para los diferentes períodos de retorno con respecto al registro histórico de la estación hidrométrica Racarrumi.

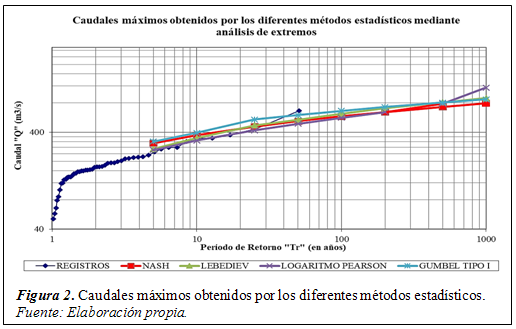
La figura 2 indica que los resultados de los caudales máximos ajustados a las distribuciones teóricas Nash, Lebediev, Logaritmo Pearson Tipo III y Gumbel Tipo I, para los diferentes períodos de retorno con respecto al registro histórico de la estación hidrométrica Racarrumi,tienden a tener valores extremos debido al aumento del período de retorno. Esto se debe a que en algunos años de los registros históricos se presentaron valores atípicos sobre todo en los eventos de máximas descargas de caudales.

De las distribuciones indicadas en la figura 2, la que presenta mejor ajuste respecto al registro es la distribución Gumbel Tipo I.

Tabla 3

Resumen de los caudales máximos obtenidos con el programa HecHmsa partir de las estaciones pluviométricas como elementos hidrológicos aportantes.

Fuente: Elaboración propia.

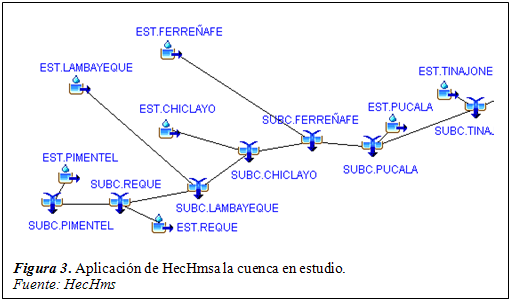
La tabla 3 muestra los caudales máximos obtenidos con el programa HecHmsa partir de las estaciones pluviométricas como elementos hidrológicos de aporte a la cuenca del río Chancay. Para lograr tal fin se modelo el proceso tal y como se indica en la investigación de Arriola, Bejarano, Arbulú, Coronado, & Sotomayor (2017)pues mencionan que al emplear un modelamiento hidrológico precipitación – escorrentía o también llamado lluvia – caudal permite generar los hidrogramas de salida en cada estación pluviométrica de manera confiable y muy cercana a un evento extremo.

Desde la figura 4 hasta la figura 10 se muestran los hidrogramas obtenidos en cada elemento hidrológico ó estación meteorológica por medio de la simulación hidrológica como referencia pues el análisis se realizó para distintos eventos extremos. Cabe indicar que cada pico o valor máximo de todos los hidrogramas es el caudal máximo obtenidopara una duración de lluvia de 210 minutos, excepto en la estación Reque que fue un tiempo de 240 minutos.

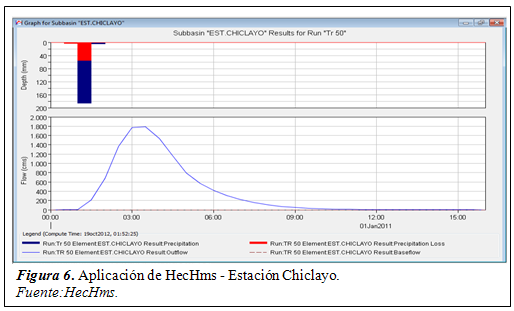
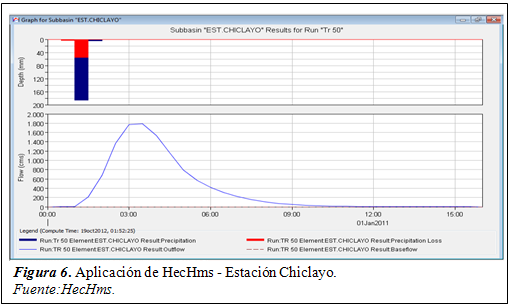
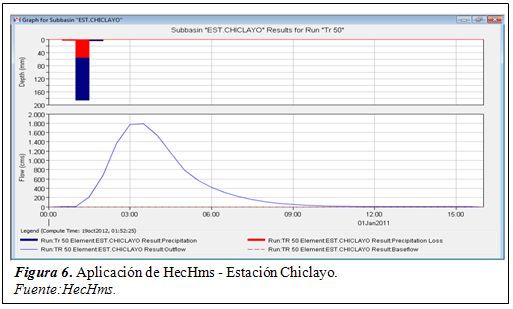
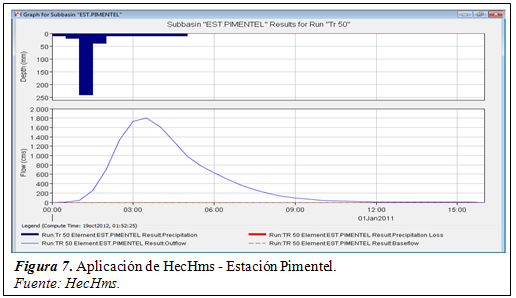
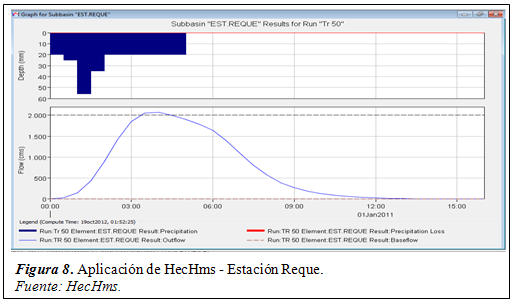
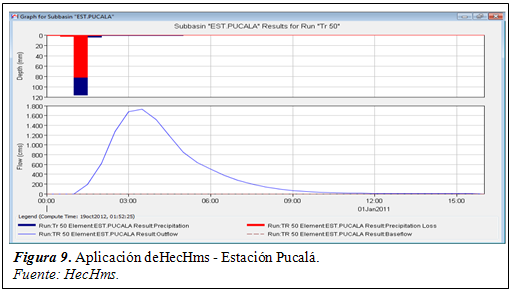
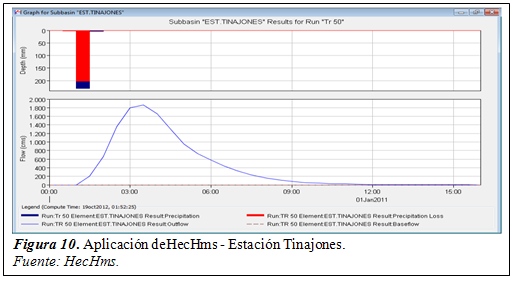
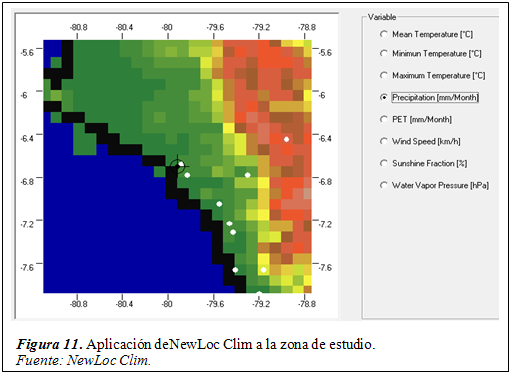
Tabla 4

Resumen de los valores del número de curva para cada subcuenca de aporte.

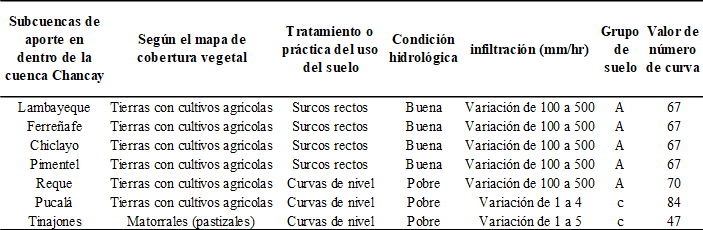
Fuente: Elaboración propia.

En la figura 11, se presenta la aplicación del programa New Loc Clima v1.10 a la zona de estudio cuya ubicación por cada estación ha servido para establecer los rangos de número de curva según las características indicadas en la tabla 4, es decir cobertura vegetal, tratamiento del uso del suelo, la condición hidrológica y grupo de suelo.

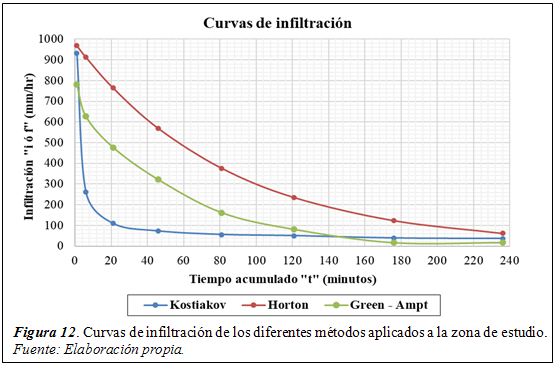
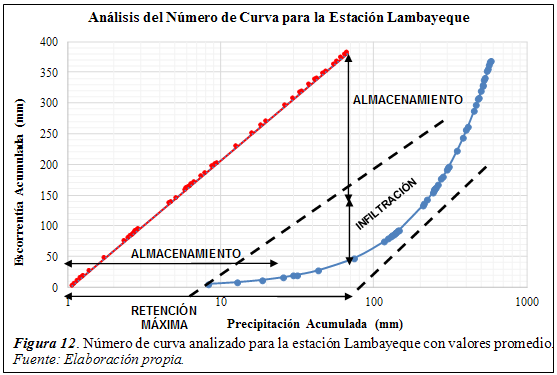
Las infiltracionessegún las figuras 12 y13, se determinaron por medio de ensayos de campo como se describió anteriormente con los anillos concéntricos de Munz y luego la aplicación de los modelos de Kostiakov, Horton y Green – Ampt para los datos medidos en campo, esto permitió escoger los valores promedio de infiltración y se determinaron que los grupos predominantes de suelos para variaciones de infiltración de 100 mm/hr a 500 mm/hr son del tipo “A” y para variaciones de infiltración de 1 mm/hr a 4 mm/hr le corresponde el tipo “C”.

Tabla 5

Resumen de los valores de los caudales máximos obtenidos con el método del número de curva para cada subcuenca de aporte dentro de la cuenca Chancay – Lambayeque.

Fuente: Elaboración propia.

Luego se muestran en la tabla 5, los resultados de los caudales máximos obtenidos con el método del número de curva para las estaciones en análisis a partir del análisis previo de las curvas de infiltración para la zona en estudio.

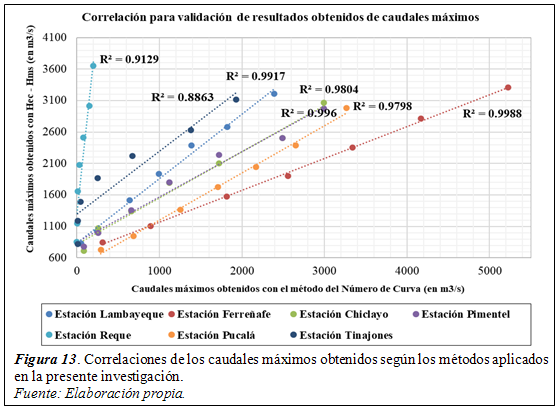
Finalmente se realizó una correlación del tipo lineal como se puede apreciar en la figura 13, que es la más aceptable para validarresultados en orden creciente al aumentar el tiempo o período de retorno, obteniéndose que si existe una muy buena correlación en todas la estaciones de hasta 99.88% de certeza de tener un muy buen ajuste por ejemplo en la estación Ferreñafe, excepto en la estación pluviométrica Tinajones que presentó una certeza de 88.63% que sin embargo para casos prácticos sería aceptable puesto que se está tomando una probabilidad de 95% y un nivel de significancia del 5% en los datos iniciales de precipitaciones y caudales de los registros históricos.

4. Discusión

La investigación se sustenta en un estudio realizado por Chin (2019), esta publicación hace referencia al modelo de infiltración a partir del método del Número de curva que están muy relacionados en la generación de hidrogramas de escorrentía para amplios rangos de aplicación, esto ayudó a que se obtengan los hidrogramas de cada subcuenca ó elemento hidrológico seleccionados dentro de la cuenca del río Chancay tal y como se sustenta en el estudio realizado por Arriola, G., Bejarano, L., Arbulú, J., Coronado, O., & Sotomayor, G. (2017), sin embargo como menciona Chin (2019) hasta la actualidad no existe ningún límite respecto a la tasas de infiltración dentro de una cuenca por lo que podría ser inconsistentes con las mediciones que se puedan realizar a corto plazo, se recomendaría en futuras investigaciones realizar un monitoreo con equipos instrumentados in situ que permitan medir las capacidades de infiltración horarias y diarias para validar aún más los datos recopilados en la presente investigación.

Otras investigaciones desarrolladas por Moret-Fernández, D., & Latorre, B. (2017) y Moret-Fernández, D., Latorre y otros (2019) y Peña-Sancho, C., Ghezzehei, T. A. y otros (2017), indican que se deben determinar cuevas de retención que definan la relación entre el contenido volumétrico y el potencial matricial que son de mucha importancia para caracterizar el comportamiento hidráulico de un suelo, proponen además desarrollar modelos y ecuaciones de infiltración para las zonas de estudio, sin embargo con los resultados presentados en esta investigación no sería tan preciso establecer un modelo definitivo debido a que la cuenca en estudio presenta una diversidad de tipos y texturas de suelo y por ende se creyó conveniente tomar valores promedios de capacidad de infiltración, esto permitió obtener los número de curva para cada elemento hidrológico con sus respectivas curvas de infiltración hasta de 240 minutos, este procedimiento concuerda en cierta forma conlas publicaciones de Chandramouli, S., & Natarajan, N. (2016) y Liu, X., Liu, C., Wang, K., & Yang, X. (2017), pues indican que se han propuesto muchos modelos de infiltración para simular las diferentes condiciones del contenido de agua iniciales y del suelo, pues como se encuentran en condiciones no uniformes pueden conducir a errores de simulación de infiltración especialmente para precipitaciones de corta duración, por ello es necesario validar los resultados con mediciones de campo.

Los objetivos que se platearon para el buen desarrollo de la investigación versaron en analizar las curvas de infiltración en las zonas de escasa información ante un eventual Fenómeno El Niño considerado como un probable evento extremo y luego los objetivos específicos, comenzando con la recolección, selección y tratamiento de la información disponible y de las características propias de la cuenca, también se realizó el procesamiento estadístico de los caudales y precipitacionespara determinar la mejor bondad de ajuste teórico y gráfico incluyendo los valores respectivos del número de curva considerando además las curvas de infiltración de los muestreos con datos de campoy finalmenteel nivel de aproximación que brinda los softwares por medio del modelo hidrológico de la cuenca denominado precipitación - escorrentía, lo cual permitirá diseñar las diversas estructuras hidráulicas en las zonas de escasa información.

5. Conclusiones

Se recolectó toda la información pertinente contando con información desde el año de 1965 al 2015 para precipitaciones y desde 1966 al 2015 para caudales.

Se realizó el procesamientodecaudales máximos y precipitaciones máximas para determinar las funciones de mejor ajuste teórico y gráfico para los diferentes períodos de retorno, escogiéndose los métodos Gumbel Tipo I y Logaritmo Pearson Tipo III.

Al aplicar el método de número de curva se determinaron los caudales máximos considerando los diferentes períodos de retorno, los cuales se muestran en los resultados de la investigación y se validaron por medio de una correlación de muy buen ajuste excepto por la estación Tinajones.

Al evaluar el nivel de aproximación que brinda el método de Número de curva se puede concluir que para estimar los caudales máximos adecuados que permitan diseñar las diferentes obras hidráulicas en la Cuenca del río Chancay es necesario conocer al menos 25 años de registros históricos para poder realizar pronósticos de caudales máximos adecuados y que se ajusten a la realidad.

Se recomienda realizar un estudio comparativo de los caudales máximos en diferentes cuencas del norte para establecer patrones hidrológicos confiables que permitan diseñar adecuadamente las diferentes infraestructuras hidráulicas.

6. Referencias

Arriola, G., Bejarano, L., Arbulú, J., Coronado, O., & Sotomayor, G. (2017). Influencia del proceso de acorazamiento en la socavación de los pilares del puente Reque. Revista Científica Ingeniería: Ciencia, Tecnología e Innovación. Obtenido de http://revistas.uss.edu.pe/index.php/ING/article/view/730.

Chandramouli, S., & Natarajan, N. (2016). A Comparative Study on the Infiltration Characteristics of Soils in Srikakulam District, Andhra Pradesh, India. Asian Journal of Water, Environment & Pollution, 13(1), 73–79. https://doi.org/10.3233/AJW-160010

Chin, D. A. (2019). Anomalous behavior of the curve-number infiltration model. Journal of Irrigation and Drainage Engineering, 145(4), [06019002]. https://doi.org/10.1061/(ASCE)IR.1943-4774.0001381.

Liu, X., Liu, C., Wang, K., & Yang, X. (2017). A simple analytical infiltration model for short-duration rainfall. Journal of Hydrology, 555, 141–154. https://doi.org/10.1016/j.jhydrol.2017.09.049.

Moret-Fernández, D., & Latorre, B. (2017). Estimate of the soil water retention curve from the sorptivity and β parameter calculated from an upward infiltration experiment. Journal of Hydrology, 544, 352–362. https://doi.org/10.1016/j.jhydrol.2016.11.03.

Moret-Fernández, D., Latorre, B., Giner, M. L., Ramos, J., Alados, C. L., Castellano, C., López, M. V., Jimenez, J. J., & Pueyo, Y. (2019). Estimation of the soil hydraulic properties from the transient infiltration curve measured on soils affected by water repellency. CATENA, 178, 298–306. https://doi.org/10.1016/j.catena.2019.03.031.

Peña-Sancho, C., Ghezzehei, T. A., Latorre, B., González-Cebollada, C., & Moret-Fernández, D. (2017). Upward infiltration–evaporation method to estimate soil hydraulic properties. Hydrological Sciences Journal/Journal Des Sciences Hydrologiques, 62(10), 1683–1693. https://doi.org/10.1080/02626667.2017.1343476.