INFLUENCIA DEL PROCESO DE ACORAZAMIENTO EN LA SOCAVACIÓN DE LOS

PILARES DEL PUENTE REQUE

INFLUENCE OF PROCESS OF DREADNOUGHT IN THE SCOUR OF THE PILLARS

BRIDGE REQUE

1. Guillermo Gustavo Arriola Carrasco

2. Luis Miguel Bejarano Trujillo

3. José del Carmen Arbulú Ramos

4. Omar Coronado Zuloeta

5. Gioconda del Socorro Sotomayor Nunura

Resumen

El presente trabajo de investigación tiene como objetivo mostrar cómo influye el proceso de acorazamiento en la socavación de pilares de puentes aplicado dicho proceso a un caso real: Puente Reque, pues esta estructura es de vital importancia para el acceso vial con la parte sur de la Región Lambayeque, pues como se recuerda en nuestro país, durante el Meganiño 1982 y 1983, caracterizado por fuertes crecidas fluviales especialmente en la costa norte, resultaron afectados y/o destruidos 55 puente y con la llegada del Meganiño de 1997 y 1998, de similares características, los datos en la infraestructura vial fueron también considerados y hubo 58 puentes destruidos y 28 puentes afectados. Prácticamente la totalidad de las fallas ocurridas en ambos meganiños tuvo su origen en problemas de hidráulica fluvial, pues como indican las estadísticas mundiales los puentes fallan principalmente por problemas de hidráulica fluvial y uno de los principales factores que influyen en este problema es la “Socavación”, entonces a partir de ahí diversos estudios han indicado que cuando se erosiona el fondo del cauce, remueve el material del lecho y del alrededor de los pilares aumentando considerablemente la socavación dependiendo del material que se va depositando, dicho efecto se denomina acorazamiento, finalmente el transporte de sedimentos de los materiales gruesos que cubren a los finos va disminuyendo hasta llegar a una condición estable en función del tiempo.

Abstract

The present work of research have as aims show how affects the process of dreadnought in the scour of bridge piers applied to a real case: Bridge Reque, because this structure is vital importance for road access to the southern part of the Lambayeque region, since as noted in our country during the meganiño 1982 and 1983, characterized by strong river flooding especially in the north coast were affected and destroyed 55 bridge and with the arrival of Meganiño 1997 and 1998, of similar characteristics, the data on road infrastructure were also considered and were 58 bridges destroyed and 28 bridges affected. Almost all failures occurred in both Meganiños originated in fluvial hydraulics problems, because as global statistics indicate bridges fail mainly fluvial hydraulic problems and one of the main factors that influence this problem is the "Scour " then from there several studies have indicated that when the bottom river is eroded, removed bed material and around piers scour increases considerably the scour depending on the material to be deposited, this effect is called dreadnought, finally the sediments transport of the coarse materials that cover to the sediments fine goes decreasing to reach a stable condition in function of time.

Palabras claves: Socavación, Caudal, Pilar, Acorazamiento, Río Chancay.

Key words: Scour, Flow, Pillar, Dreadnought, Chancay River .

1. EAP Ingeniería Civil. Facultad de Ingeniería, Arquitectura y Urbanismo. Ing. Docente Tiempo Parcial de la E.A.P. de Ingeniería Civil de la Universidad Señor de Sipán. Chiclayo. Lambayeque. Perú. garriola@crece.uss.edu.pe.

2. EAP Ingeniería Civil. Facultad de Ingeniería, Arquitectura y Urbanismo. Empresa BT Consultores y Contratistas Generales E.I.R.L. Chachapoyas. Amazonas. Perú. luis13_btla@hotmail.com

3. EAP Ingeniería Civil. Facultad de Ingeniería Civil, Sistema y Arquitectura. Dr. Msc. Ing. Docente Principal de la Universidad Nacional Pedro Ruiz Gallo. Lambayeque. Perú. ingjar323@hotmail.com.

4. EAP Ingeniería Civil. Facultad de Ingeniería, Arquitectura y Urbanismo. Dr. Msc. Ing. Coordinador de EAP Ingeniería Civil de la Universidad Señor de Sipán. Chiclayo. Lambayeque. Perú. descicivil@uss.edu.pe.

5. Facultad de Ingeniería, Arquitectura y Urbanismo. Dr. Docente Tiempo Completo. Jefe de la Unidad de Investigación de la FIAU de la Universidad Señor de Sipán. Chiclayo. Lambayeque. Perú..

gioconsdasn@uss.edu.pe

1. Introducción

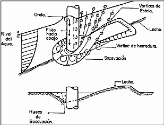
Se conoce como el efecto de “Acorazamiento” al proceso morfológico en el cual, conforme el fondo del cauce se erosiona, el material grueso se acomoda de tal forma que cubre al material fino, es decir poco a poco se va acorazando el fondo hasta tal punto que el transporte de sedimentos va disminuyendo llegando a una condición estable.

Este efecto es importante considerarlo para el cálculo de la socavación debido a que conforme va pasando el tiempo este acorazamiento presenta resistencia al flujo y genera mayor variación en el transporte de sólidos en suspensión y de arrastre como por ejemplo en un pilar de un puente.



Luego vista la problemática de que el Puente Reque se encuentra ubicado en una zona que está constantemente asociado a efectos de erosión y por ende de socavación y por otro lado que los pilares del puente ofrecen oposición constante y variable al flujo debido al caudal, es entonces necesario estudiar la influencia del proceso de acorazamiento en la socavación de los pilares del puente mencionado, pues com se recuerda en nuestro país, durante el Meganiño 1982 – 1983, caracterizado por fuertes crecidas fluviales especialmente en la costa norte, resultaron afectados o destruidos 55 puentes. Con la llegada del Meganiño de 1997 – 1998, de similares características al antes mencionado, los datos en la infraestructura vial fueron también considerados y hubo 58 puentes destruidos y 28 puentes afectados.

En el departamento de Lambayeque, dentro de los puentes que afectó dicho fenómeno se encuentra el Puente Reque ubicado en el cruce del Río Reque con la carretera Panamericana Norte en el Km 772 + 789.33, el cual, en los últimos 50 años se erigió en más de tres oportunidades. En el año 2009, según el estudio del Ministerios de Transporte y Comunicaciones se amplió el puente 50.00 m. sobre el acceso izquierdo, con el que incrementaría su capacidad hidráulica a 2000 m3/s, para un período de retorno de 500 años, siendo la nueva luz del puente 150.00 m. con dos pilares intermedios, incluyendo la cimentación profunda con pilotes de cada pilar. El acceso al área de estudio puede ser realizado por vía terrestre y vía aérea. Por vía terrestre se llega a través de la carretera Panamericana Norte (la cual se encuentra asfaltada) desde Lima hasta la localidad de Reque, por vía aérea se opta por los vuelos Lima – Chiclayo, teniendo la última parada en el aeropuerto internacional José Quiñones (Chiclayo).

2. Materiales y Métodos

2.1. Objetivo general y específicos

Estudiar la influencia del proceso de acorazamiento en la socavación de los pilares del Puente Reque, luego los objetivos específicos como fin del objetivo general de la investigación fueron:

• Analizar y evaluar la influencia del proceso de acorazamiento en la socavación de los pilares a partir de las diversas formulaciones que se emplean actualmente para recomendar, de ser el caso, la metodología que cuente con estimaciones razonables para determinar la socavación total.

• Seleccionar los métodos adecuados que se basen en ecuaciones de predicción que permitan estimar adecuadamente la profundidad de socavación donde intervenga la influencia del acorazamiento del material en los pilares.

• Aplicar los métodos adecuados para la determinar socavación en base a la influencia del acorazamiento del material en los pilares del Puente Reque y en función de los resultados obtenidos plantear adecuadas propuestas de solución.

2.2. Hipótesis del Problema

La hipótesis de la investigación se planteó de la siguiente manera: La influencia del proceso de acorazamiento permitirá determinar adecuadamente la socavación en los pilares del Puente Reque estimada a partir de las formulaciones actuales.

2.3. Variables

Variable única: Acorazamiento del río en el Puente Reque.

Indicadores: Caudal del Río, Geometría del Río y del Puente, Tirante hidráulico, Área hidráulica, Pendiente y Cotas, Distribución del material que componen el cauce (Granulometría), Nivel de socavación. Sedimentos.

2.4. Tipo de investigación

El tipo de investigación que se aplicará es del tipo aplicada.

3. Resultados

3.1. Información básica

Descripción general de la cuenca

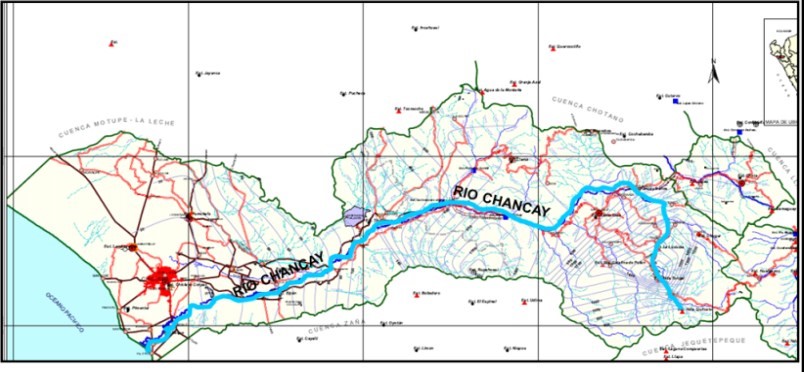
La cuenca hidrográfica del Río Chancay – Lambayeque, se ubica en el norte del Perú, políticamente su territorio corresponde a los departamentos de Lambayeque y Cajamarca. Limita por el Norte con la cuenca del Rio La leche, por el sur con la cuenca del Río Jequetepeque – Zaña, por el este con la cuenca del Río Chotano y por el oeste con el Océano Pacífico. El área de drenaje de la cuenca hasta la Bocatoma Racarumi es de 5404.18 Km².



El rio Chancay pertenece a la vertiente del Pacífico, es de régimen irregular y está conformado por los ríos Tacamache y Perlamayo que nacen en la Cordillera Occidental de los Andes; desde sus nacientes hasta su desembocadura en el mar, su longitud es de 170.00 Km; en su recorrido recibe aportes eventuales principalmente de los ríos Cañad, San Lorenzo, Cirato y Cumbil. El rio Chancay, al pasar cerca de la ciudad Reque, ofrece un cauce de ancho variable entre los 120.00 m y 500.00 m, con áreas que han sido aprovechadas por los lugareños para fines agrícolas. Además el clima es cálido y seco, las precipitaciones pluviales son escasas manifestándose generalmente en forma de garúa.

La temperatura del aire en la cuenca es variable, así se tiene que en la estación Lambayeque el promedio anual es de 21°C y en Tinajones es de 23°C los valores mínimos registran un promedio anual de 17.9°C en Lambayeque, 18.3°C en Tinajones y 11°C en Huambos; en tanto que los promedios máximos anuales alcanzan los 25.8°C en Lambayeque.

Respecto a la información pluviométrica se contó con un número importante de estaciones meteorológicas que disponen de información pluviométrica, como Precipitaciones máxima en 24 horas se han utilizado 16 Estaciones Pluviometrías tales como: Lambayeque, Ferreñafe, Chiclayo, Pucalá, Tinajones, Reque, Pimentel, Puchaca, Tocmoche, Llama, Huambos, Santa Cruz, Chancay Baños, Chugur, Quilcate, Cochabamba.

En cuento a la información hidrométrica del rio Chancay, los caudales han sido registrados desde el año 1914 en forma continua, habiendo sido analizada a lo largo de los años por diferentes Instituciones. Actualmente ETECOMSA tiene a su carga la operación y registro de la estación Chancay, la información prácticamente sin interrupciones. Para los propósitos de la presente investigación se utilizará sólo los registros tomados de la Bocatoma Racarumi por ser considerados como datos de consistencia para el respectivo análisis (1966 – 2009).

3.2. Estudio Hidrológico

Análisis de la información pluviométrica y distribución de frecuencias

Las fuentes de obtención de los datos de Precipitación, son las estaciones Pluviométricas, constituyéndose esta información en el fundamento principal de todo el análisis pluviométrico, luego los resultados obtenidos están en dependencia de la cantidad de los datos disponibles. El análisis pluviométrico se desarrolló con datos correspondientes a las Precipitaciones máximas diarias anuales de las siguientes estaciones Pluviométricas:

N° ORDEN	ESTACION PLUVIOMETRICA	LATITUD	LONGITUD	ALTITUD (m.s.n.m.)	CUENCA
1	LAMBAYEQUE	6°42´ S	79°55´ W	18	CHANCAY
2	FERREÑAFE	6°38´ S	79°47´ W	67	CHANCAY
3	CHICLAYO	6°46´ S	79°50´ W	27	CHANCAY
4	PUCALA	6°45´ S	79°36´ W	85	CHANCAY
5	TINAJONES	6°40´ S	79°29´ W	240	CHANCAY
6	REQUE	6°53´ S	79°51´ W	21	CHANCAY
7	PIMENTEL	6°50´ S	79° 56´ W	4	CHANCAY
8	PUCHACA	6°21´ S	79°28´ W	500	LA LECHE
9	TOCMOCHE	6°25´ S	79°22´ W	1250	LE LECHE
10	LLAMA	6°30´ S	79° 07´ W	2090	CHANCAY
11	HUAMBOS	6°27´ S	78°58´ W	2200	CHANCAY
12	SANTA CRUZ	6°37´ S	78°57´ W	2000	CHANCAY
13	CHANCAY BAÑOS	6°34´ S	78°52´ W	1600	CHANCAY
14	CHUGUR	6°40´ S	78°40´ W	2744	CHANCAY
15	QUILCATE	6°49´ S	78°44´ W	3100	CHANCAY
16	COCHABAMBA	6°28´ S	78°53´ W	1800	CHANCAY



El análisis está orientado a encontrar la distribución de frecuencias de valores extremos que más se ajuste a los datos observados para cada estación, obteniéndose los resultados de acuerdo al comportamiento de la serie de datos de cada estación. Este análisis incluye los valores extremos de los años extraordinarios de 1983 y 1998. El registro que se tomó en cuenta para dicho análisis es desde el año 1965 al 2009. También se consideró como las estaciones índices para completar los datos faltantes de las otras estaciones a las siguientes: Lambayeque, Huambos y Chugur por ser todas las estaciones cercanas unas de otras y por su consistencia de los datos que se han registrado. De acuerdo a los resultados obtenidos, presentamos en los siguientes cuadros comparativos las precipitaciones para los dos métodos analizados, para diferentes años de periodo de retorno:

Análisis de la información hidrométrica

Antes de proceder al análisis se debe contar con los caudales máximos diarios mensuales anuales del Río Reque, debido a que no se dispone de registros de aforos de dicho río, por eso se ha recurrido a la información hidrométrica disponible histórica de las Estaciones Carhuaquero – Racarumi (1914 al 2009). Para efectos de la presente investigación se ha utilizado solo los datos registrados en la estación Racarumi que registra las descargas del río Chancay (1966 al 2009). Con los datos de los caudales máximos se ha realizado el análisis estadístico de frecuencias con la finalidad de obtener las descargas para períodos de retorno de 5, 10, 25, 50, 100, 200, 500, 1000. Estos datos también permitirán calcular los parámetros hidráulicos a definir para la evaluación hidráulica del Puente Reque. Para determinar los caudales máximos se emplearon los métodos estadísticos y un modelo de simulación hidrológica con el programa HEC – HMS v3.5.

Se presenta a continuación una tabla con los resultados obtenidos:

T (años)	METODO DE NASH	METODO DE LEBEDIEV	METODO DE LOG PEARSON III	METODO DE GUMBEL TIPO I
5	313.20	287.55	263.97	327.96
10	378.63	379.98	324.24	403.37
25	463.08	520.15	405.31	546.44
50	526.61	549.70	469.05	609.24
100	590.18	700.60	535.77	672.03
200	653.88	805.75	605.74	734.83
475	733.58	959.72	686.31	813.19
500	738.31	971.45	731.49	817.84
1000	802.33	1035.77	1038.27	880.64

En la figura siguiente se puede observar que la distribución que se acerca a la línea de registro es la del Método de Lebediev.

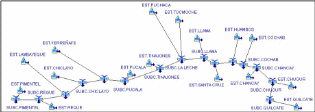
Para el procedimiento de simulación nos basamos principalmente en los aportes que recibe el curso principal (Río Chancay) en zonas altas a más de 2000 m.s.n.m. como Llama, Chugur, Quilcate, Santa Cruz y Huambos, pues las estaciones que se encuentran en estas zonas son las que registran precipitaciones altas, en comparación con las estaciones que se encuentran en menor altitud y muy cerca a las costas del Océano Pacífico, pero que sin embargo en épocas de máximos eventos como el ocurrido en 1998 (Fenómeno del Niño) aumentaron considerablemente su registro en ese año y de esta manera generó un caudal de 1998 m3/s en las inmediaciones del Puente Reque ocasionando la caída del mismo en ese año. Entonces al no contar con la información hidrométrica de cada una de las quebradas de aporte a cada subcuenca (es decir que cada una de las 16 estaciones que se emplearon en el presente estudio se tomaron como subcuencas); se procedió entonces a desarrollar un modelo de Precipitación – Escorrentía para la obtención de caudales de avenida en dichas quebradas. Es por eso que el modelo se ha basado en dichas características ya que el programa Hidrologyc Modeling System (HMS v.3.50 para Windows) emplea las precipitaciones máximas en 24 horas para generar los caudales en los lugares de interés que se quieran analizar.

A continuación, se presentan el desarrollo del esquema hidrográfico simulado con el programa HEC - HMS v. 3.50 (ver imagen), así como el resultado para un periodo de retorno de 50 años en la Estación Reque el cual arrojo un caudal de 2075.00 m3/s.

Luego el caudal de diseño considerado que asumimos es de 2075.00 m3/s, basándonos en el modelo de simulación que emplea el programa HEC –HMS v.3.50, dicho programa emplea el proceso lluvia – escorrentía, que considera el aporte e influencia de las 16 subcuencas en todo el trayecto del Río Chancay hasta la zona de interés (Puente Reque), que a diferencia de los métodos estadísticos que solo consideran los datos hidrométricos de la Estación Racarumi.

3.3. Estudio hidráulico del Puente Reque

Tras la obtención del cálculo de caudales, para los periodos de retorno analizados, se ha procedido a elaborar el modelo hidráulico de simulación del flujo. El resultado de la aplicación de los caudales de cálculo al modelo hidráulico ha sido la determinación de los niveles alcanzados por el flujo y las velocidades del Río Chancay en la zona del Puente Reque, la longitud de análisis es de 1500 m., con un ancho de 600.00 m. La metodología que se ha seguido consiste en la construcción de modelos hidráulicos unidimensionales, en régimen permanente de los cauces.

La modelización se ha realizado utilizando el programa HEC – RAS v.4.00 del U.S. Army Corps of Enginners. Sobre el modelo del cauce actual del Rio Chancay en el Puente Reque, se han determinado los niveles alcanzados por la corriente de agua para periodos de 5, 10, 25, 50, 100, 200, 500, y 1000 años, en las secciones de cálculo y por último se han representado los tramos críticos del río, propensas a desbordamientos, sedimentación y erosión por estrangulamiento del cauce (zona del puente).

Con los caudales obtenidos por simulación hidrológica mostrado en el correspondiente ítem del Estudio

Hidrológico de la presente investigación, para períodos de recurrencia de 5, 10, 25, 50, 100, 200, 500 y 1000 años, se aplicó el modelo hidráulico de simulación del flujo con el programa HEC – RAS v.4.00. El HEC – RAS (Hydrologic Engineering Center – River Analysis System, traducido al español Centro de Ingeniería Hidrológica – Sistema de Análisis de Ríos), es una aplicación que permite la modelación hidráulica en régimen permanente y no permanente de cauces abiertos, ríos y canales artificiales, desarrollada por el Centro de Ingeniería Hidrológica del Cuerpo de Ingenieros de la Armada de los E.E.U.U. (U.S. Army Corps of Enginners). Con los cálculos hidráulicos realizados se presenta entonces a continuación las características hidráulicas en la sección de interés (Eje del Puente Reque).

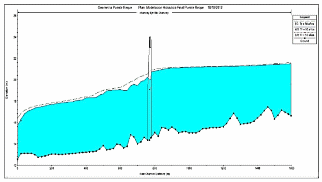
Fuente: Elaboración Propia

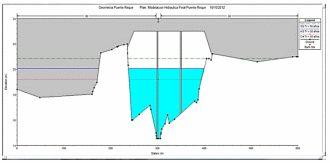
Fuente: Elaboración Propia

3.4. Proceso de acorazamiento en los pilares del puente Reque

Para que ocurra el acorazamiento de un cauce es necesario que el flujo pueda arrastrar los granos finos del material del cauce, pero no los más gruesos, sino las partículas pequeñas, incapaces de resistir el paso del agua, van siendo lavadas o transportadas por la corriente, lo que hace que afloren partículas de mayor tamaño que sí pueden resistir a las fuerzas de arrastre y sustentación debidas al flujo; de este modo, por la permanencia de las partículas gruesas, se va formando una especie de empedrado o coraza en la superficie del lecho, que protege del arrastre o acarreo al material fino subyacente.

El proceso de acorazamiento es fundamentalmente un problema de inicio de arrastre o de transporte naciente; dicho proceso debe tenerse en cuenta al tratar con sedimentos no cohesivos de granulometría no uniforme y extendida, ya que en este tipo de sedimentos no se tiene una condición única o situación promedio de transporte incipiente, como acontece con material uniforme, sino que pueden darse varias condiciones de transporte incipiente: Si las partículas de diámetro mínimo están a punto de ser movidas por el flujo, se está en la condición llamada punto inferior de transporte incipiente; por el contrario, cuando el flujo está a punto de mover las partículas de diámetro máximo, se alcanza entonces el punto superior de transporte incipiente. Entre ambos puntos o situaciones extremas de transporte incipiente, dependiendo de las características del flujo y de las del material del cauce, también podrán suceder otras situaciones intermedias de transporte incipiente. Por tanto, entre los puntos inferior y superior de transporte incipiente es donde ocurre el fenómeno de acorazamiento y, por consiguiente, podrán darse distintos grados de acorazamiento, según los tamaños de las partículas que permanezcan formando la coraza o armadura del cauce.

Sin embargo, dado el carácter aleatorio de la turbulencia en el flujo de agua, siempre existirá la posibilidad de que cualquier grano sea arrastrado por el flujo y bajo igualdad de condiciones, la probabilidad de que una partícula no sea arrastrada y forme parte de la coraza, q, será mayor para las partículas gruesas que para las finas. Gessler obtuvo experimentalmente dicha probabilidad, analizando el material erosionado y el que formaba coraza.

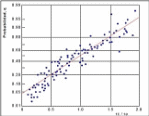
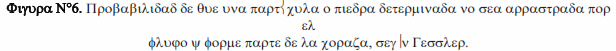
3.5. Método simplificado para calcular el acorazamiento en pilares de puentes.

Como en casi todos los temas de ingeniería fluvial e hidráulica, solo existen por el momento algunos métodos aproximados para modelar el acorazamiento, aunque se ha avanzado mucho en el tema, se recalca que este es un fenómeno complejo y, tal vez por ello, los métodos son cada vez más sofisticados. Cuando el material que constituye un cauce es de granulometría extendida, los procesos de erosión y acorazamiento son simultáneos: para cierta socavación de la cota del fondo, una parte del material es removida y trasportada por la corriente, mientras otra contribuye a la formación de la coraza.

Así, si el material del cauce está constituido por un total de “n” fracciones de diferentes tamaños, de las cuales las fracciones más grandes no pueden ser movidas por el esfuerzo cortante que produce el flujo, es posible modelar el proceso del acorazamiento calculando el área de la superficie del fondo que va quedando cubierta por los granos de “n” tamaños y determinar esta área acorazada, se obtiene primero el volumen del sedimento que queda inmóvil conforme el fondo se degrada; se calcula después el área ocupada por dicho volumen, suponiendo que el espesor de la coraza es equivalente al diámetro medio de los granos más grandes.

PARAMETROS PARA ESTIMAR LA INFLUENCIA DEL PROCESO DE ACORAZAMIENTO EN LA SOCAVACION DE PILARES DE PUENTES EN FUNCION AL DIAMETRO MODIFICADO
FORMULA	PARAMETRO	SIMBOLO	UNIDAD
AREA ACORAZADA (Af)	POROSIDAD DE LA MUESTRA	ϵ	Adimensional
	ELEVACION DEL FONDO EN EL TIEMPO	Δz(t)	m
	FACTOR DE FORMA DE LA PARTICULA	fs	Adimensional
	FACTOR DE DIAMETRO DE LA PARTICULA		Adimensional
DIAMETRO DEL MATERIAL MAS PEQUEÑO NO ARRASTRADO POR EL FLUJO (D1)	TIRANTE DEL ESCURRIMIENTO	h	m
	PENDIENTE DEL CAUCE	S	m/m
	DENSIDAD RELATIVA DEL MATERIAL DEL SUELO	Ss	Adimensional
MODIFICACIÓN DE LA GRANULOMETRÍA (Di)	DIAMETRO ORIGINAL (D50)	Dio	mm
	DIAMETRO DEL MATERIAL MAS PEQUEÑO NO ARRASTRADO	Dic	mm
	FUNCION f	f	Adimensional

Fuente: Elaboración propia



Esto se muestra de manera esquemática donde se nota que el área de la superficie acorazada se incrementa con la degradación del cauce y que tal proceso termina cuando se llega a formar una capa completa de material grueso sobre la superficie, la cual se conoce como coraza. El desarrollo presentado a continuación se basa en el planteado originalmente por Karim (1983); la versión formal del método puede verse en Karim y Holly (1986). Al hacer la revisión bibliográfica se discutió que la coraza contiene sedimentos de todos los tamaños del material original del cauce, pero en el presente análisis se supondrá que en la superficie del lecho hay una parte de material constitutivo de la coraza y otra susceptible de moverse; esto significa que las partículas finas que se encuentran entre otras más grandes no contribuyen a la formación de la coraza, ya que algunas de ellas podrán pasar a formar parte del trasporte de sedimento de un momento a otro y otras quedarán protegidas por las partículas de la coraza.

Cabe resaltar que las limitaciones del método para estimar el área acorazada son las siguientes:

1. El área acorazada se incrementa únicamente cuando hay erosión; en caso de que en un tramo del río se tuviera depósito de sedimento, el área acorazada debería disminuir si granos finos cubren a los de la coraza. Dado que el cálculo de esta condición es muy complicado, en el procedimiento aquí descrito se considera que el área acorazada es constante cuando hay depósito, y se incrementa si hay erosión.

2. Existe un esfuerzo cortante máximo que un fondo acorazado resiste; dicho esfuerzo se puede estimar usando el procedimiento de Cruickshank y García (1976) basado en el método de Gessler (1967) o con las expresiones propuestas por Maza y García (1990). El área acorazada se incrementa si el cortante actuante es menor que este cortante máximo. Por el contrario, si el cortante actuante en un tramo dado rebasa el máximo que resiste la coraza, esta se rompe; es decir, todos los granos se mueven, lo cual equivale a que el área acorazada sea cero.

3.6. Socavación de los pilares del Puente Reque para pilares complejos

Los componentes de socavación para pilares complejos se encuentran ilustrados en la siguiente figura. La figura se complementa con la definición de variables. Nótese que la placa la placa de cimentación puede encontrase por encima de la superficie del agua, en la superficie del agua o en el lecho.

Determinación del componente de socavación debido al pilar

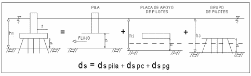
El componente de socavación para la pila se debe calcular cuando la placa de cimentación y el grupo de pilotes se encuentra dentro del flujo y existe una porción suficiente de la pila expuesta a velocidades y profundidades que pueden producir socavación. El primer cálculo se refiere al cálculo del “ds” del pilar, utilizando el ancho y largo del pilar, cuya ecuación es la siguiente:

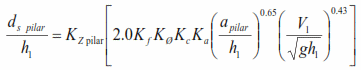
Donde:

ds pilar: socavación para el pilar en el flujo.

h1: profundidad del flujo de aproximación al inicio de los cálculos, en metros (m).

f: distancia entre el borde de la placa de cimentación y la cara de la pila en metros (m).

Kz pilar: es el coeficiente para tomar en cuenta la altura del pilar sobre el lecho y el efecto de la obstrucción que produce la placa de cimentación; definiéndose una distancia “f” igual a la distancia entre la cara frontal de la pila y el extremo del voladizo de la placa.

Kf: Factor que depende de la forma del pilar.

KØ: Factor que depende del ángulo de ataque del flujo.

Kc: es el factor de corrección por la forma del lecho.

Ka: Factor de corrección por acorazamiento del sedimento del lecho, cabe señalar que el valor mínimo de Ka es 0.4.

Determinación del componente de socavación debido a la placa de cimentación (losa de fundación) La necesidad de calcular la socavación debida a la placa de cimentación o placa de amarre de pilotes, se da cuando esta placa se encuentra expuesta al flujo desde la etapa inicial del diseño, o como producto de la degradación a largo plazo, de la socavación por contracción y/o de la socavación atribuida al pilar, sobre la placa. Tal como se describe a continuación, existe la situación que debe considerarse al estimar la socavación causada por la placa de cimentación. Cabe resaltar que en este caso se deberá considerar un factor de influencia llamado factor de ancho del pilar “Kw”.

Como el fondo de la placa de cimentación se encuentra bajo el nivel del lecho se empleará la estrategia de tratar la placa o la fundación expuesta, como si fuera un pilar de poca altura en un flujo de poca profundidad, considerando la altura en el flujo igual a la altura expuesta de la placa; es decir, la altura medida desde el fondo del lecho hasta el nivel superior de la placa. La fórmula para determinar la socavación en este componente es la siguiente:

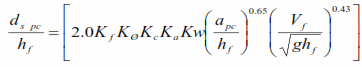
Todos los parámetros de esta ecuación, son los mismos que los empleados en las ecuaciones anteriores, con la variante del parámetro Kw, que se calcula considerando lo siguiente:

Determinación del componente de socavación debido al grupo de pilotes

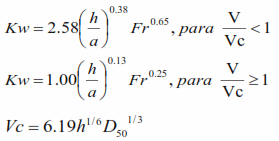
Las investigaciones realizadas por Salim y Jones y por Smith han proporcionado la base para determinar la profundidad de socavación debida al grupo de pilotes, tomando en consideración el espaciamiento entre ellos, el número de filas de pilotes y un factor de altura que toma en consideración la longitud del pilote expuesto al flujo.

Luego el ancho efectivo de una pila única es el producto del ancho proyectado, multiplicado por el factor de espaciamiento y un factor de alineamiento de las filas (usando para el caso especial de las pilas alineadas solamente). Finalmente la ecuación para determinar la socavación debido al grupo de pilotes

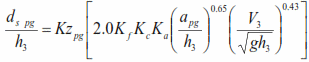
Donde:

Kz pg: es un factor de altura del grupo de pilotes dado en la siguiente figura:

Todos los demás parámetros de la fórmula son los mismos que los empleados en las ecuaciones anteriores, con la variante del parámetro “Kzpg”, que se calcula considerando lo expresado anteriormente.

3.7. Aplicación de la metodología a los pilares del puente Reque

Luego teniéndose como datos los principales parámetros hidrológicos (precipitaciones, caudales) y los parámetros hidráulicos (tirantes, velocidades, niveles de energía) se procedió a calcular el diámetro del material más pequeño que no es arrastrado por el flujo y compararlo con el diámetro del material que se depositará en ambos pilares producto de la erosión del material del cauce. Entonces bajo estos criterios se continuó con la modificación de la granulometría para estimar adecuadamente el parámetro “Ka” calculado partir de la influencia del proceso de acorazamiento en la socavación, pues es uno de los principales factores que intervienen en cada una de las fórmulas basadas en la superposición de componentes para pilares complejos, y además el criterio para estimarlo aún está en estudio pues a pesar de ser repetitivo en cada una de las fórmulas es necesario establecer rangos para su aplicación a nivel regional. Finalmente, a manera de resumen se muestran los resultados obtenidos para estimar el parámetro Ka, que influye directamente en el proceso de socavación en los pilares del Puente Reque:

Fuente: Elaboración Propia

CUADRO DE RESUMEN COMPARATIVO DE ESTUDIO DE SOCAVACION PARA EL PILAR ANTIGUO DEL PUENTE REQUE PARA UN PERIODO DE RETORNO (Tr = 50 AÑOS)		UNIDAD
PARAMETROS	SOCAVACION TOTAL
ESTUDIO GEOLÓGICO, GEOTÉCNICO, HIDROLÓGICO Y DE HIDRÁULICA FLUVIAL PARA EL REFORZAMIENTO Y AMPLIACIÓN DEL PUENTE REQUE" (MTC - AÑO 2005)	13.50	m
METODOLOGIA PLANTEADA POR LA HEC (HYDROLOGYC ENGINEERING CENTER – CENTRO DE INGENIERIA HIDROLOGIA DEL CUERPO DE INGENIEROS DE LA ARMADA DE E.E.U.U.)	14.91	m
METODOLOGIA PLANTEADA POR LA HEC (HYDROLOGYC ENGINEERING CENTER – CENTRO DE INGENIERIA HIDROLOGIA DEL CUERPO DE INGENIEROS DE LA ARMADA DE E.E.U.U.) INCLUYENDO LA MODIFICACION DEL FACTOR Ka	17.91	m

Fuente: Elaboración Propia

CUADRO DE RESUMEN COMPARATIVO DE ESTUDIO DE SOCAVACION PARA EL PILAR PRODUCTO DE LA AMPLIACION DEL PUENTE REQUE PARA UN PERIODO DE RETORNO (Tr = 50 AÑOS)		UNIDAD
PARAMETROS	SOCAVACION TOTAL
ESTUDIO GEOLÓGICO, GEOTÉCNICO, HIDROLÓGICO Y DE HIDRÁULICA FLUVIAL PARA EL REFORZAMIENTO Y AMPLIACIÓN DEL PUENTE REQUE" (MTC - AÑO 2005)	14.00	m
METODOLOGIA PLANTEADA POR LA HEC (HYDROLOGYC ENGINEERING CENTER – CENTRO DE INGENIERIA HIDROLOGIA DEL CUERPO DE INGENIEROS DE LA ARMADA DE E.E.U.U.)	13.94	m
METODOLOGIA PLANTEADA POR LA HEC (HYDROLOGYC ENGINEERING CENTER – CENTRO DE INGENIERIA HIDROLOGIA DEL CUERPO DE INGENIEROS DE LA ARMADA DE E.E.U.U.) INCLUYENDO LA MODIFICACION DEL FACTOR Ka	17.77	m

Fuente: Elaboración Propia

Finalmente se presenta a manera de propuesta un gráfico para encontrar directamente en función de ancho del pilar y el diámetro modificado de las partículas, el factor “Ka” influenciado por el acorazamiento del río para encontrar adecuadamente la socavación total en pilares de puentes.

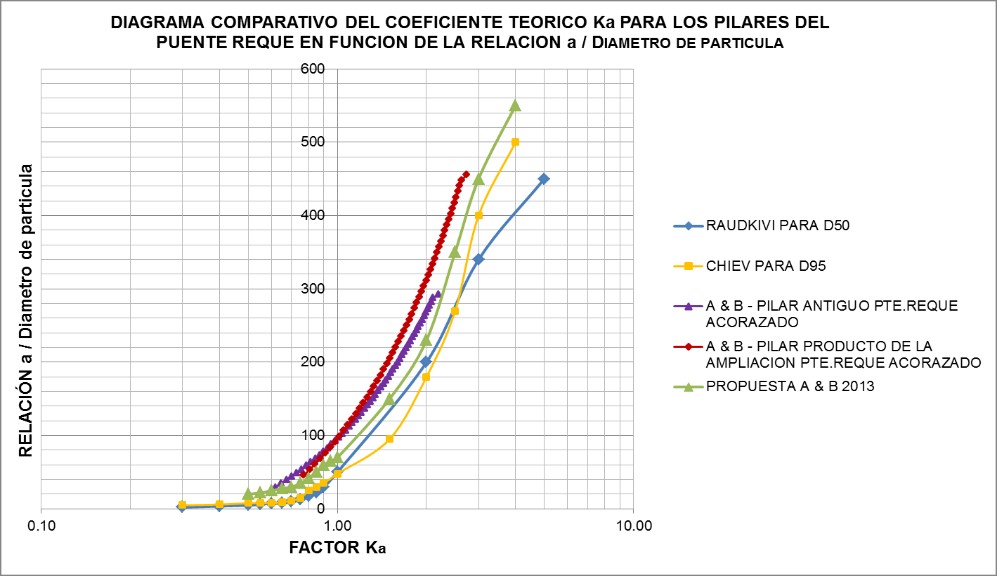
Fuente: Elaboración Propia

4. Discusión de los resultados obtenidos

Como se aprecia en la figura la línea verde corresponde a nuestra propuesta en base a la relación a/dpf (ancho del pilar con el diámetro de la partícula modificado) y otras metodologías ya estudiadas por ingenieros de otros países, y como también se hace notar la curva generada es válida para pilares de puentes con anchos y/o anchos equivalentes de hasta 4.00 metros y diámetros de partículas de hasta 2.00 milímetros modificados a partir de la influencia del acorazamiento.

Es necesario indicar que se requiere para una mayor validación y exactitud de los resultados que se obtengan, la realización de un modelo hidráulico a escala bajo ciertas condiciones y características para validar los resultados ya obtenidos y ampliar de esta manera los rangos de aplicación de la influencia del acorazamiento en el cálculo de la socavación de pilares de puentes a partir de la estimación del parámetro “Ka” (factor que depende del acorazamiento del lecho del río)

El acorazamiento de manera general es a veces lenta y casi despreciable, reduciéndose muchas veces a determinarse en un solo parámetro, entonces bajo este criterio se puede concluir que dicha hipótesis es válida cuando el río no aporta sedimentos, no obstante para el caso del Puente estudiado (Puente Reque), que se encuentra ubicado en la Cuenca del Río Chancay si es significativo el acorazamiento ya que como se muestra en los resultados la socavación aumenta en 3.00 metros a más para ambos pilares.

Por último el criterio adecuado para estimar la socavación total sobre todo en pilares complejos debe basarse en el buen juicio de un ingeniero, por decir la metodología HEC – 18 es la más sobresaliente de todas, puesto que introduce a sus cálculos, factores que netamente influyen en el proceso de socavación (Forma de Pila, Angulo de Ataque del Flujo, Ancho de la Pila, Velocidad, Sedimento, D₅₀, Gravedad), además adhiere a sus fórmulas las características geométricas de los dos Pilares (Longitud, Ancho, Altura, Espesor de la Pila, de la Losa de Cimentación y Pilotes). Así también optimiza variables influyentes en la socavación, para analizarla producto del Grupo de Pilotes, Losa de Cimentación y Pila, y calcula la socavación total estimada sumando las 03 variables encontradas.

5. Conclusiones

1. Según los resultados obtenidos del Ensayo de Mecánica de Suelos y comparados con los de “Estudio Geológico, Geotécnico Hidrológico y de Hidráulica Fluvial Para el Reforzamiento y Ampliación del Puente Reque” (MTC – Año 2005), se comprueba que tanto el Pilar Antiguo como el Pilar Producto de la Ampliación del Puente Reque se encuentran desplantados sobre suelo areno limoso (en menor proporción niveles de grava a más de 20 metros de profundidad).

2. En el informe hidrológico correspondiente al “Estudio Geológico, Geotécnico Hidrológico y de Hidráulica Fluvial Para el Reforzamiento y Ampliación del Puente Reque” (MTC – Año 2005), utilizan un registro de aforos para el periodo comprendido entre 1914 a 1998; datos que corresponde a las estaciones de aforo Carhuaquero – Racarrumi, lo cual carece de sustento, debido a que desde 1914; los datos pertenecen sólo a la estación Carhuaquero. Por lo tanto, los caudales máximos del Rio Chancay, utilizados en el citado estudio, consideran 52 datos de caudales indebidamente tomados para determinar el caudal de diseño en la Ampliación del Puente Reque.

3. Los mayores valores de los caudales resultantes de la modelación del proceso Precipitación – Escorrentía, obedece al aporte de 16 Sub Cuencas de Aforo (que se han utilizado para la presente investigación) existentes a lo largo del Río Chancay hasta las inmediaciones del Puente Reque, tales como; Lambayeque, Ferreñafe, Chiclayo, Pucalá, Tinajones, Reque, Pimentel, Puchaca, Tocmoche, Llama, Huambos, Santa Cruz, Chancay Baños, Chugur, Quilcate, Cochabamba y el caudal de diseño considerado es de 2075.00 m3/s, correspondiente a un periodo de retorno de 50 años. Valor que influye claramente en la velocidad, 3.91 m/s. Dato escogido para iniciar los cálculos de socavación.

4. Respecto a la influencia del proceso de acorazamiento en la socavación de pilares puentes se puede decir que es un fenómeno complejo que aún no está totalmente estudiado, sin embargo la propuesta de la presente investigación conduce hacia un aporte significativo para el cálculo adecuado de dicho fenómeno modificando el parámetro Ka (factor de sedimento) que incluye la granulometría modificada a partir de la granulometría de los sedimentos del lecho del río y de una gráfica para estimar el factor de acorazamiento del lecho de un río (en función de la relación de a/D) para un pilar complejo de un puente.

5. Sobre el Pilar producto de la ampliación del Puente Reque se puede concluir que no presenta problemas de socavación bajo la influencia del acorazamiento, ya que el nivel de cimentación del pilar es de 28.70 metros, encontrándose muy por debajo de los niveles de socavación obtenidos. El nivel de socavación calculado, en este Pilar es de 17.77 metros.

6. Para darle un mayor ajuste a las fórmulas para estimar la profundidad de socavación ya que es una variable no determinada en su exactitud puesto que depende de muchas otras como el caudal, granulometría, ancho de los pilares, forma del pilar, profundidad del flujo, velocidad, entre otros, entonces se recomienda por ello plantear en futuras investigaciones la influencia de dichos parámetros que se validen a través de modelos matemáticos e hidráulicos ya que los métodos existentes para calcular la socavación frecuentemente predicen un valor conservador con el objetivo de incorporar algún grado de seguridad en el diseño de un puente o en la evaluación de un puente ya construido, sin embargo este factor de seguridad es desconocido.

7. Se ha dado un paso más en la investigación del Fenómeno de Socavación del Puente Reque en su condición actual (Ampliado 2008 – 2009) y se incita a otros profesionales a continuar con investigaciones relacionadas a la influencia del acorazamiento y de otros factores que influyan en la socavación en pilares complejos, tanto del Puente Reque como de otros puentes, cuyo daño involucre cuantiosas pérdidas económicas y/o humanas.

6. Referencias Bibliográficas

Arbulú R. J. (2009). Socavación en pilares de puentes: Análisis comparativo de metodologías predictivas. Lambayeque. Perú. Publicaciones de la Universidad Nacional Pedro Ruiz Gallo.

Arneson L.A., Zevervengen L.W., Lagasse P.F & Clopper P.E. (2012). Evaluation Scour at Bridges. Estado de Virginia. Estados Unidos. Publicaciones de la Universidad del Estado de Virginia.

Arriola C. & Bejarano T. (2013). Estudio de los Métodos de análisis basados en la Superposición de los Componentes de Socavación para pilares complejos aplicados al Puente Reque. Chiclayo Perú. Revista Científica TZHOECOEN. Volumen 5. N°1. Publicaciones de Universidad Señor de Sipán.

Berezowsky V. M. & Jiménez C. A. (1995). Método Simplificado para calcular el Proceso de Acorazamiento en Cauces. Ciudad de México. México. Publicaciones de la Universidad Autónoma de México.

Graf H. (1971). Hydraulics of sediment transport. New York. Estados Unidos. Publicaciones de Mc Graw Hill.

Maza A. J. & García M. (1990). Características del acorazamiento para distribuciones lognormal corregida y logarítmica. Montevideo. Uruguay. Memorias del XIV Congreso

Latinoamericano de Hidráulica.

Villón B. M. (2004). Hidrología. Lima. Perú. Ediciones Villón.

Villón B. M. (2008). Hec-Hms Ejemplos. Lima. Perú. Ediciones Villón.

Villón B. M. (2009). Hec-Ras Ejemplos. Lima. Perú. Ediciones Villón.